Ride Frequency (Sprung mass natural frequency) really is meaningless overall, however it can be used to represent specific attributes of the suspension system.
What it is is the rate expressed in cycles per minute (cpm) or cycles per second (Hz) at which the sprung mass (The weight of car supported by 1 tire less the weight of the tires/wheels/hubs/brakes) would bounce up and down at infinitely. Since a car is not 4 independent masses, and there are inherent frictional losses in the system a car will not actually bounce forever but whatever bouncing it does will be at the suspensions natural frequency.
It is calculated for a vehicle by taking the effective spring rate at the wheel (Wheel Rate or WR) and dividing it by the Sprung Mass (SM). Deriving the formula from the actual formula for spring natural frequency (1/2pi*sqrt(K/m), where K is the spring rate, m is mass suspended) results in the equation for use on a vehicle of
NF = 187.8*sqrt(WR/SM) in cpm or NF = 3.13*sqrt(WR/SM) in Hz. For Hz we just divide by 60s to convert (1cycle/min X 1min/60seconds = 1 cycle / 60 seconds).
The 187.8 is just the aggregate of all the constants that pop out of the sq-rt when you convert from lbf to lbm, consider gravitational constants, and do the 1/2pi math.
Ok now we understand where natural frequency comes from but why do we care? It is a single number that considers the spring rate, the motion ratio, and the corner weight of the vehicle and gives you an immediate idea of the stiffness of the suspension and the wheel travel you can expect to use. Because it compares wheel rate to actual corner weight it applies across all vehicle types/suspension types/spring types. So my pullrod bellcrank dual A-arm suspension on a 1500lb car could be directly compared to the beam axle air spring on a Semi truck.
It also considers the motion ration inherently. My MG midget has 875 lb/in front spring coils on a car that weighs 1600lbs. If I tell you that with no other information you will think suspension is super stiff because that is nearly 2x the corner weight. But the MR of the suspension make the ride frequency ~2.5, Stiff but not unbearable. When you make suspension changes to the Motion Ratio, or spring rate you can use natural frequency to compare the changes. If i want to keep the overall ride compliance roughly the same but am exploring several different spring options I can simply aim for the same natural frequency to solve it.
Because a car at rest is exposed to 1G of load (and ignoring pre-load on the springs, and things like tender springs and progressive or digressively wound springs) we can use natural frequency to directly determine the droop/sag of the suspension. This is because the ratio of WR/SM if we are using spring rate in lbs/in and SM in lbs we are left with the ratio actually being inches of travel at 1G (Lbs/in x 1 / lbs = in). So if we solve the natural frequency equation for SAG = WR/SM = 3.13^2xNF^2. I've plotted the relationship between natural frequency and SAG bellow. Again spring preload and progressive suspension designs will impact the actual amount of SAG but for a idealized suspension this is how the relationship works.
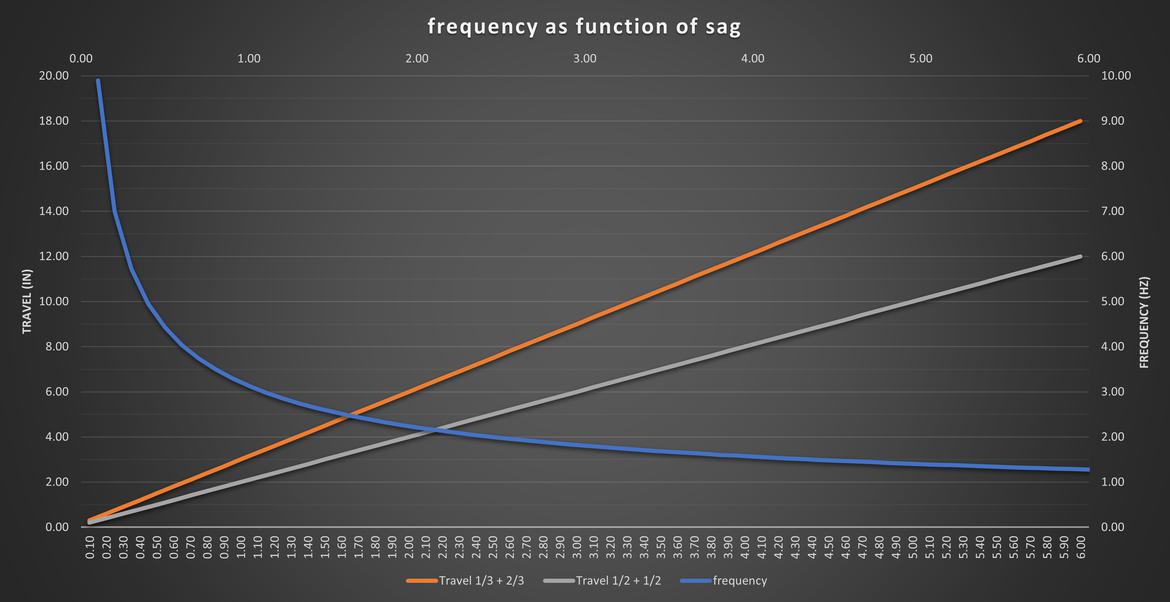
Also I've included the expected total travel for the 2 prevailing thoughts on the relationship between SAG and bump travel. That's probably for another discusion but in my experience for linear suspensions designed to only use the bumpstops to protect the suspension from breakage on low CG vehicles total travel is 1/2 SAG, 1/2 bump travel. Many people use 1/3 SAG, 2/3 Bump. Things like the Miata have huge SAG values but relatively little travel before they get into the bumpstops. Also many production cars will have large SAG but use progressively wound coils to stiffen the suspension as it travels. So again this is just rough guides for understanding different suspensions.
So why don't we just use the direct ratio WR/SM. No idea, this makes us sound smarter and confuses people more which if we are honest is the goal of Engineering, because if people knew how much rounding and idealization Engineers used in deriving all the formulas we actual use to design stuff they would question us a lot more. Also because when you get into damper design suspension frequency is an important part of identifying the amount of damping to target. Damper design is a subject I don't have a lot of understanding on so someone else would have to elaborate on that, I just turn knobs indiscriminately until it feels nice.
I'll make another post soon showing the math behind the spreadsheet, I suspect the big deal for most will be tackling the push/pull rod and bellcrank stuff, and the details of that are rough at this point. I know the effective ratios I need, what I don't have yet is the angles I am targeting between the belcrank "arms" and the pullrods/shocks to give linear to progressive spring rates rather then digressive. I will go into that with detail when I get to it. I have what I need for now to build the suspension arms and pickup points. I can give the spreadsheet to people who are interested but it's not a "clean" spreadsheet to use. I developed it organically and illogically. It's not like one of those online put your numbers in here and it vomits out pretty graphs and such.







































