The old HP vs TQ debate.

Torque = force * radius (lb*ft). So torque is force around an axis. Engines produce torque. Transmission multiplies torque through radius ratios. Wheels apply force to the ground at radius. The mass of the vehicle is accelerated by the force applied. That force comes from the torque the engine generates through a radius.

MattGent wrote: Please show me a gear train that multiplies or divides power output.

Not sure if serious? All of them ... that aren't 1:1... unless I feel like being a shiny happy person, in which case it's still multiplied... by 1

wvumtnbkr said: it is not possible to make Force = lb-ft.

Because torque is rotational and not linear the "ft" comes into play. Linear force is lb (technically slug or lbf but you know what I mean) and by (simplified) definition acts on the center of mass of an object, rotational force is lb-ft b/c by definition (again, simplified) a rotational force is not acting on the center of mass of an object, thus it has to be a certain radius from the center of mass.

nocones wrote: Torque = force * radius (lb*ft). So torque is force around an axis. Engines produce torque. Transmission multiplies torque through radius ratios. Wheels apply force to the ground at radius. The mass of the vehicle is accelerated by the force applied. That force comes from the torque the engine generates through a radius.

Except that we are also looking at force applied over time and distance. Which is power. Applying the same force (torque) over the same distance for a shorter time period requires more power.

Swank Force One wrote: https://grassrootsmotorsports.com/forum/grm/stupid-and-unrealistic-which-is-faster-question/75502/page1/

I don't think I ever bothered to finish reading that.....did you ever discover that a longer gear than a 15-25mph increase can be good if you have enough power?

jsquared wrote:

MattGent wrote: Please show me a gear train that multiplies or divides power output.

Not sure if serious? *All of them* ... that aren't 1:1... unless I feel like being a shiny happy person, in which case it's still multiplied... by 1

None of them. Power throughput is constant, excluding losses. All the transmission does is trade torque for RPM, either up or down. No power is multiplied, only torque, and that graph is bunk.

In reply to jsquared:

Thanks? I was simply explaining how/why F=ma has units of lb but torque has units of lb-ft and generally is is OK to talk about torque as supplying that force despite it being lb-ft. One would divide by the tire radius which for most passenger vehicles is close enough to 1' for it to be ignored in conceptual discussions.

I was not intending to get into the middle of the e-thug contest that is TQ vs HP.

jsquared wrote: Practical example: You have two cars with 300 ft-lbs of torque and the same gearing, but with different power output since they make torque in different parts of the power band. One completes a quarter of a mile in 14 seconds. One completes a quarter of a mile in 12 seconds. They both performed the same amount of work (same distance and same torque applied), but one of them did it in less time. Same work done in less time means more power was used. Car that covered the distance in less time did so due to POWER, not torque.

This "practical example" is flawed. The higher power engine would of course be quicker. It would have different shift points, at higher rpm and higher ground speed, even with the same transmission, so its integrated "torque-to-ground" force curve would be much higher. Same distance, more torque applied, to use your terms.

Optimizing the torque to the ground vs. speed curve will give you the best use of available power from a given engine/tranny combo. Of course the engine with more power will be able to accelerate the car quicker, as it can take better use of gearing.

An interesting corollary is that the optimum shift point may not be the same rpm for each gear change, assuming you don't hit the rev limiter.

And taken to its limit, we would all want to run a CVT. Power through-put is constant, with the transmission adjusting to keep the engine at its peak power rpm.

jsquared wrote:

MattGent wrote: Please show me a gear train that multiplies or divides power output.

Not sure if serious? *All of them* ... that aren't 1:1... unless I feel like being a shiny happy person, in which case it's still multiplied... by 1

wvumtnbkr said: it is not possible to make Force = lb-ft.

Because torque is rotational and not linear the "ft" comes into play. Linear force is lb (technically slug or lbf but you know what I mean) and by (simplified) definition acts on the center of mass of an object, rotational force is lb-ft b/c by definition (again, simplified) a rotational force is not acting on the center of mass of an object, thus it has to be a certain radius from the center of mass.

nocones wrote: Torque = force * radius (lb*ft). So torque is force around an axis. Engines produce torque. Transmission multiplies torque through radius ratios. Wheels apply force to the ground at radius. The mass of the vehicle is accelerated by the force applied. That force comes from the torque the engine generates through a radius.

Except that we are also looking at force applied over time and distance. Which is power. Applying the same force (torque) over the same distance for a shorter time period requires more power.

Linear force is just Lbs (force). It is NOT slugs. Slugs is mass.

In reply to Nocones:

If you had an engine that only produced torque, the vehicle would maintain steady state operation. In other words, it would stay at one wheel speed.

for example, if I apply 50 pounds of force to a 2' long wrench (torque), I will be applying 100 lb-ft to the nut. The nut will not accelerate. The Nut will continue to turn at the same velocity unless there is an outside force OR the "rate" that the torque is applied changes.

MattGent is right. Gearing does not multiply POWER, it multiplies torque.

He's also right, and I'm also embarrassed that I did not catch this earlier... the graph is bunk. The Y axis should not be POWER. Tractive effort would make it correct.

Of course none of that changes what was discussed earlier... POWER/area under the POWER curve is what we are after here. No need to get hung up on TQ.

If anything a graph of POWER vs. Road Speed would look like the opposite as lower gears (higher ratios) are inherently less efficient.

yamaha wrote:

Swank Force One wrote: https://grassrootsmotorsports.com/forum/grm/stupid-and-unrealistic-which-is-faster-question/75502/page1/

I don't think I ever bothered to finish reading that.....did you ever discover that a longer gear than a 15-25mph increase can be good if you have enough power?

I decided it was easier to just gear the car to do whatever top speed i wanted, and then increase boost as necessary.

nocones wrote: In reply to jsquared: Thanks? I was simply explaining how/why F=ma has units of lb but torque has units of lb-ft and generally is is OK to talk about torque as supplying that force despite it being lb-ft. One would divide by the tire radius which for most passenger vehicles is close enough to 1' for it to be ignored in conceptual discussions. I was not intending to get into the middle of the e-thug contest that is TQ vs HP.

Oops, I misread that. My bad.

wvumtnbkr said: Linear force is just Lbs (force). It is NOT slugs. Slugs is mass.

Crap. I suck today. That's what happens when I try to do stuff I haven't done in ~10 yrs

MattGent said: This "practical example" is flawed. The higher power engine would of course be quicker. It would have different shift points, at higher rpm and higher ground speed, even with the same transmission, so its integrated "torque-to-ground" force curve would be much higher. Same distance, more torque applied, to use your terms.

Explain how the higher power engine "put more torque to the ground" when both engines have the same peak torque and gearing. When you start factoring in shift rpm and such, you are bringing time/distance into the equation, and force with time and distance means power.

MattGent said: An interesting corollary is that the optimum shift point may not be the same rpm for each gear change, assuming you don't hit the rev limiter.

That's what the graph is for. When the curves cross, you don't want to shift at redline. E.g. for my MS Paint graph (which is decidedly NOT bunk, if you disagree I suggest you strap your vehicle to a chassis dyno and do pulls in different gears and plot them by road speed instead of rpm), you would shift 1st to 2nd earlier than redline, where the two curves cross.

ProDarwin said:

If anything a graph of POWER vs. Road Speed would look like the opposite as lower gears (higher ratios) are inherently less efficient.

? 1st gear applies more power to the ground than 5th, hence the 5th gear curve has a lower peak (and is further to the right, since it operates across faster speeds than 1st). Again, strap a vehicle down to a chassis dyno and plot the power in each gear.

Whatever you are building is going to pull like crazy no matter what!

In my mind, torque is the muscle and HP is how fast the muscle is being delivered. Your torque is pretty flat and maxed out between 3500 and 5000 rpm, so its a question of delivering as much of this quantity of muscle as fast as possible.

Once you reach 5000 rpm, both the muscle and rate of deliver start to drop off, so it is time to put you back in the sweet-spot. So, grab a gear and go back to the start of the sweet spot and repeat.

If it were my guess, I would attach it to gear ratios that allowed the RPM to drop from 5000 to 3500 rpm every time I pulled the lever. That puts you in the fat end of the torque curve with the max slope on the HP curve.

jsquared wrote:

ProDarwin said: If anything a graph of POWER vs. Road Speed would look like the opposite as lower gears (higher ratios) are inherently less efficient.

? 1st gear applies more power to the ground than 5th, hence the 5th gear curve has a lower peak (and is further to the right, since it operates across faster speeds than 1st). Again, strap a vehicle down to a chassis dyno and plot the power in each gear.

He's right. Power will be the same.

1st will have very high wheel TQ, very low wheel RPM
2nd will have less TQ, more RPM
...
6th will have very low TQ, a ton of RPM

When you convert the combo of TQ and RPM to POWER, it's going to be the same in all gears.

Your graph should have Tractive Effort, Acceleration, or Wheel TQ on the Y axis.

You have to have Road Speed as the X-Axis to find the ideal shift point, because you have to compare output to the ground at each vehicle linear MPH, so you know (for example) whether 2nd gear or 3rd gear outputs more at 70 mph, then 75, then 80, etc. Plotting according to road speed means you are measuring power, as you are accounting for distance and time as well as torque force. I was going to Excel spreadsheet it but I am having trouble with my equations and getting the damned chart maker to invert my X and Y axes for the gear chart so it's easier to visualize the output-v-roadspeed issue with actual data instead of an MS Paint squiggle. My 12-hr shift is done and barracks internet is crap so I will have to postpone that until tomorrow

NOHOME wrote: Whatever you are building is going to pull like crazy no matter what! In my mind, torque is the muscle and HP is how fast the muscle is being delivered. Your torque is pretty flat and maxed out between 3500 and 5000 rpm, so its a question of delivering as much of this quantity of muscle as fast as possible. Once you reach 5000 rpm, both the muscle and rate of deliver start to drop off, so it is time to put you back in the sweet-spot. So, grab a gear and go back to the start of the sweet spot and repeat. If it were my guess, I would attach it to gear ratios that allowed the RPM to drop from 5000 to 3500 rpm every time I pulled the lever. That puts you in the fat end of the torque curve with the max slope on the HP curve.

That's what seems to make sense, but its not correct. (as I just learned) The gear multiplication in the lower gear is greater than the next higher gear. Not winding it out to higher RPMs, you're leaving a ton of torque at the driveshaft unused.

I couldn't resist doing some Excel work. I really hope no malice/attitude comes through with this. I am simply sharing my understanding of the question being how to calculate when to shift.

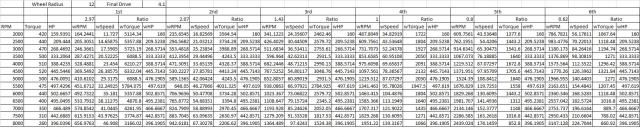
I read torque at 500 rpm increments off of Curtis's chart. I theoretically hooked this up to a GM aftermarket T56 as referenced on the T56 wiki page (2.97, 2.07, 1.43, 1.00, .80, .62 ratios) with a 4.10 final drive. I theoretically used a 24" diameter tire so I could just express wheel torque without conversion. I calculated Wheel RPM, Wheel Speed (MPH), Wheel Torque (lb-ft) and Wheel HP at each 500 rpm value. The model does not take into account different driveline losses for each gear.
Wheel RPM = Engine RPM / (Gear Ratio * Final Drive Ratio)
Wheel Speed = Wheel RPM * 2Pi(Tire Radius / 12) * 60 / 5280
Wheel Torque = Engine Torque * Gear Ratio * Final Drive Ratio
Wheel HP = Wheel Torque * Wheel RPM / 5252

The results are shown in the table below.

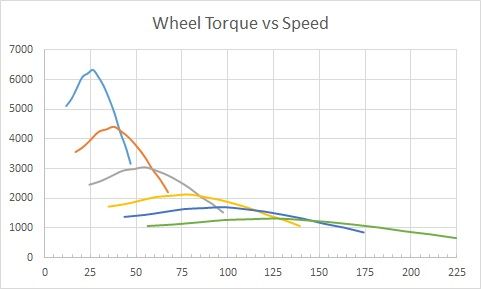
This chart shows Wheel Torque plotted against Wheel Speed (Vehicle speed). Torque here since the tire is 24" diameter is equivalent to Tractive Force. Shift points would be at chart crossovers.

This Chart shows Wheel HP plotted against Wheel Speed (Vehicle speed). Note that in each gear the chart is identical to the HP the engine makes. I have not accounted for driveline losses. In reality WHP would be less than Engine HP and lower numerical gears would have lower WHP due to losses. Again ideal shift points are crossovers between each gear.

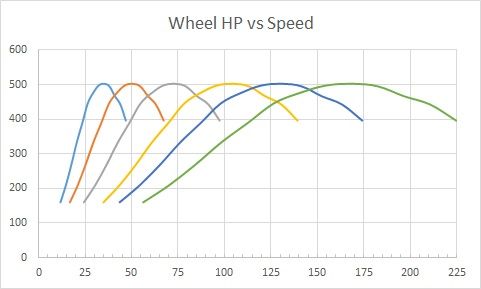
In this analysis shift points where calculated to occur as shown
Shift Speed Shift RPM
1st 40 6800
2nd 60 7200
3rd 80 6500
4th 115 6600
5th 145 6750

These points are calculated to be the same based on either WHP or WTQ.

So after looking at it I come away with the feeling that it doesn't mater which way you do it. Both cause the same results. Calculating WHP or WTQ will result in the same data. This is predictable because the relationship is the same HP = Torque * RPM / 5252. If you used Wheel RPM instead of Speed you could convert Wheel Torque and Wheel RPM to HP and generate the WHP chart. Is there something about this I'm missing?

nocones wrote: Is there something about this I'm missing?

Nope.